فضاء متجهي

الفضاء الاتجاهي أو الفضاء المتجهي أو الفضاء الشعاعي كائن أساسي في دراسة الجبر الخطي.[1][2][3] هو مجموعة من عدة متجهات والتي هي كائنات يمكن إضافتها مع بعضها البعض وضربها بأعداد، التي يطلق عليها كميات قياسية في هذا السياق. غالبا ما تكون الكميات القياسيات أعدادا حقيقية، ولكن بالإمكان اختيار فضاءات اتجاهية مع كميات قياسية من أعداد مركبة أو أعداد نسبية أو حتى حقول عامة. عمليتا جمع المتجهات وضرب متجهة ما في كمية قياسية ينبغي لهما أن تحققا مجموعة من المتطلبات تدعى موضوعات جاءت أسفله. فضاء المتجهات الإقليدية هو مثال على الفضاءات المتجهية حيث يمكن أن تمثلن كميات فيزيائية مختلفة كالقوى وغيرها.
فعندما تعتبر المتجهات مع العمليات المطبقة عليها من جمع وضرب قياسي وبعض العمليات الأخرى مثل الانغلاق والتجميعية، فإنه يوصل إلى وصف كائن رياضي يُدعى فضاءً اتجاهياً.
المتجهات في الفضاء الاتجاهي لا تمثل تحديداً متجهات هندسية بل يمكن أن تكون أي كائن رياضي يحقق بدهيات الفضاء الشعاعي. فمتعددات الحدود من الدرجة ≤n على سبيل المثال، بمعاملات حقيقية تشكل فضاءً شعاعياً.
تدرس الفضاءات المتجهية في إطار الجبر الخطي وهي مفهومة بشكل كامل من هذا المنطلق، حيث يتميز كل فضاء متجهي ببُعده. يحدد هذا البُعد عدد الاتجاهات (أو الحركات) المستقلة عن بعضها البعض داخل الفضاء المعين. قد تُضاف إلى فضاء متجهي بُنى أخرى كالمعيار والجداء الداخلي.
تاريخيا، تعود أول فكرة أدت إلى الفضاء المتجي إلى القرن السابع عشر في إطار الهندسة التحليلية والمصفوفات والمعادلات الخطية والمتجهات الإقليدية. انظر إلى جيوسيبي بيانو وإلى أعماله في هذا المجال.
حاليا، تطبق الفضاءات المتجهية في الرياضيات والعلوم والهندسة، حيث تشكلن البنية الجبرية الملائمة لدراسة أنظمة المعادلات الخطية، وتُشكلن أيضا الإطار العام لدراسة متسلسلات فورييه اللائي يستعملن بدورهن في ضغط الصور، ولتقنيات حلحلة المعادلات التفاضلية الجزئية. انظر أيضا إلى موتر ومتعدد شُعب وجبر تجريدي.
مقدمة وتعريف[عدل]
المثال الأول: الأسهم في المستوى[عدل]

|
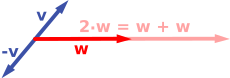
|
المثال الثاني: أزواج مرتبة من الأعداد[عدل]
المثال الثاني على الفضاءات المتجهية هو الأزواج من الأعداد الحقيقية و (الترتيب الذي جاءا فيه العددان و مهم يعني بصفة عامة. لهذا السبب سمي هذا الزوج بزوج مرتب).
تعريف شامل[عدل]
لتكن مجموعة من العناصر (ليس بالضرورة أعداد) مزودة بقانون تركيب داخلي يرمز له بـ (ليس بالضرورة الجمع المألوف)
وليكن حقل تبادلي (استعملت الرموزو لكي لا يتم الخلط بينها وبين و لكنها لا تعدو كونها مجرد رموز)
نعرف الفضاء المتجهي على أنه مجموعة مزودة بـ
- قانون تركيب داخلي يرمز له بـ
- قانون تركيب خارجي يرمز له بـ
حيث تحقق الخاصيات التالية :
| الموضوعة | المعنى |
| تجميعية الجمع | |
| تبديلية الجمع | |
| وجود العنصر المحايد للجمع داخل () الذي يحقق لكل : | |
| وجود العنصر المعاكس للجمع داخل () لكل ، والذي يحقق : | |
| توزيعية قانون التركيب الخارجي على الجمع الداخلي في | |
| توزيعية قانون التركيب الخارجي على الجمع الداخلي في | |
| توافق الجداء المعرف على مع الجداء الخارجي لـ | |
| العنصر المحايد لعملية الجداء الداخلي في يحقق لكل : |
نقول أن هو فضاء متجهي معرف على
تسمية ونرميز[عدل]
- عناصرتسمى المتجهات . تكتب عادة بحروف لاتينية صغيرة و غالبا ما تميز عن كونها مجرد أعداد برسم سهم فوق اسم المتجهة وخصوصا في الفيزياء والهندسة، أو ببساطة قد تكتب بخط غليظ
- عناصرتسمى الكميات القياسية أو كميات سُلمية (scalaire). مثل الأعداد الحقيقية أوالأعداد العقدية. عادة ما تُمَيـز عن المتجهات بكتابتها بحروف يونانية صغيرة .
التاريخ[عدل]
تنبثق الفضاءات المتجهية من الهندسة التآلفية، من خلال تقديم الإحداثيات في المستوى أو في الفضاء ثلاثي الأبعاد. في حوالي عام 1636، أسس كل من ديكارت وفيرما الهندسة التحليلية، وذلك من خلال الربط بين حلول معادلة ذات متغيرين من جهة، ونقط من منحنى في المستوى من جهة ثانية.
عرفت الفضاءات المتجهية تطورا مهما يعود فضله إلى وضع أسس فضاءات الدوال من طرف هنري لوبيغ.
أمثلة[عدل]
فضاءات الإحداثيات[عدل]
الأعداد العقدية وامتدادات حقول أخرى[عدل]
مجموعة الأعداد العقدية C تكوّن فضاء متجهيا:
(.,+,C) هو فضاء متجهي على الحقل C حيث + هو الجمع بين الاعداد العقدية المألوف و . هو الضرب المألوف بين العداد العقدية
يمكنك التحقق بنفسك ( كتمرين ) من أن هاذان القانونين + و . يحققان بدهيات الفضاء المتجهي
انظر أيضا إلى امتداد الحقول وإلى نظرية الأعداد الجبرية
فضاءات الدوال[عدل]
- (f + g)(w) = f(w) + g(w)
انظر إلى فضاء الدوال وإلى مستقيم الأعداد الحقيقية.
المعادلات الخطية[عدل]
a + 3b + c = 0 4a + 2b + 2c = 0
القواعد والبُعد[عدل]
التطبيقات الخطية والمصفوفات[عدل]
المصفوفات[عدل]

حيث تعني الجمع.
القيم الذاتية والمتجهات الذاتية[عدل]
فضاءات متجهية بُبنى إضافية[عدل]
فضاءات متجهية طوبولوجية[عدل]
فضاءات باناخ[عدل]
فضاءات هيلبرت[عدل]
تطبيقات[عدل]
التوزيعات[عدل]
تحليل فورييه[عدل]
الهندسة التفاضلية[عدل]
انظر أيضا[عدل]
مراجع[عدل]
- ^ "معلومات عن فضاء متجهي على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2017-12-09.
- ^ "معلومات عن فضاء متجهي على موقع bigenc.ru". bigenc.ru. مؤرشف من الأصل في 2019-12-10.
{{استشهاد ويب}}:|archive-date=/|archive-url=timestamp mismatch (مساعدة) - ^ "معلومات عن فضاء متجهي على موقع brockhaus.de". brockhaus.de. مؤرشف من الأصل في 2019-12-10.
| في كومنز صور وملفات عن: فضاء متجهي |



































