رسم بياني لدالة

من ويكيبيديا، الموسوعة الحرة

اذهب إلى: تصفح, بحث

في الرياضيات يعتبر الرسم البياني لدالة رياضية أو مبيانها[1] هو الخط الذي يجمع كافة النقاط (x1, x2, ..., xn, f(x1, ..., xn)).

حيث الدالة الرياضية هي :f(x1, x2, ..., xn) حيث يظهر الرسم البياني على شكل منحني أو سطح، كما يظهر في الرسم البياني أيضاً المحاور الإحداثية. الرسم البياني في نظام الإحداثيات الدريكارتية كثيراً مايرمز له بالمنحنى التخطيطي.

[عدل] أمثلة

  • مخطط التابع التابع
f(x)=\left\{\begin{matrix} a, & \mbox{if }x=1 \\ d, & \mbox{if }x=2 \\ c, & \mbox{if }x=3. \end{matrix}\right.

هو النقاط الثلاثة {(1,a), (2,d), (3,c)}.

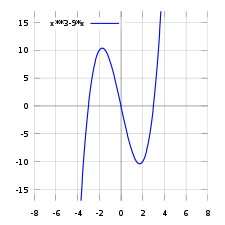
  • مخطط التابع كثير الحدود من الدرجة الثالثة التالي:
f(x)={{x^3}-9x} \!\

هو (x,x3-9x) ويكون الرسم للتابع في نظام الإحداثيات الديكارتية على الشكل الموضح:

[عدل] انظر أيضاً

[عدل] مراجع

  1. ^ [1]
بوابة رياضيات تصفح مقالات ويكيبيديا المهتمة بالرياضيات.
تم الاسترجاع من "http://ar.wikipedia.org/wiki/%D8%B1%D8%B3%D9%85_%D8%A8%D9%8A%D8%A7%D9%86%D9%8A_%D9%84%D8%AF%D8%A7%D9%84%D8%A9"
أدوات شخصية