لوغاريتم طبيعي
| لوغاريتم طبيعي | |
|---|---|
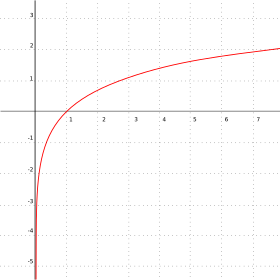 منحنى دالة اللوغاريتم الطبيعي. تتزايد الدالة ببطء إلى زائد ما لا نهاية له عندما يصير x كبيرا، بينما تذهب إلى ناقص ما لا نهاية له بسرعة كبيرة عندما يقترب x من الصفر. محور y هو خط مقارب للدالة.
| |
| تدوين | |
| تعريف الدالة | |
| دالة عكسية | |
| مشتق الدالة | على المجال |
| مشتق عكسي (تكامل) |
|
| الميزات الأساسية | |
| مجال الدالة | |
| المجال المقابل | |
| قيم محددة | |
| القيمة/النهاية عند الصفر | على اليمين: |
| نهاية الدالة عند +∞ | |
| القيمة/النهاية عند 1 | 0 |
| القيمة/النهاية عند e | 1 |
| خطوط مقاربة | |
| جذور الدالة | 1 |
| تعديل مصدري - تعديل | |
اللوغاريتم الطبيعي (بالإنجليزية: Natural logarithm) أو اللوغاريتم النِيبْيَري هي دالة لوغاريتمية للأساس e. وهي الدالة الاصلية للدالة على وتنعدم في 1. يُرمز لهذه الدالة ب Log (عدم الخلط مع log والتي ترمز لدالة اللوغاريتم العشري) أو ln
بصفة عامة.
التاريخ
[عدل]ويسمى هذا اللوغاريتم أيضا باللوغاريتم النيبيري تكريماً لعالم الرياضيات الاسكتلندي جون نابير الذي أنشأ أول الجداول اللوغاريتمية (والتي ليست في الواقع جداول اللوغاريتمات الطبيعية).
تم وضع مفهوم اللوغاريتم الطبيعي بواسطة غريغوار دو سان فنسان [الإنجليزية] و ألفونس أنطونيو دي ساراسا [الإنجليزية] قبل عام 1649. تضمن عملهم تربيع القطع الزائد الذي معادلته xy = 1 من خلال تحديد مساحة القطاعات الزائدية. تولد حلولهم دالة «اللوغاريتم الزائدي» المطلوبة التي لها خصائص مرتبطة الآن باللوغاريتم الطبيعي.
وضعت أول إشارة للوغاريتم الطبيعي من قبل نيكولاس مركاتور في عمله Logarithmotechnia المنشور في 1668، [1] على الرغم من أن مدرس الرياضيات جون سبيديل [الإنجليزية] قام بالفعل في عام 1619 بتجميع جدول لما كان في الواقع لوغاريتمات طبيعية. لقد قيل إن لوغاريتمات سبيديل كانت ذات الأساس e ، لكن هذا ليس صحيحًا تمامًا بسبب التعقيدات مع القيم المعبر عنها كأعداد صحيحة.
اتفاق حول الرموز
[عدل]يشير الرمزان "ln x" و "loge x" بشكل لا لبس فيه إلى اللوغاريتم الطبيعيّ لِـx. وقد يُفهم من الرمز "log x" دون أي ذكر صريح لأي أساس أنه لوغاريتم طبيعيّ لِـx. يشيع هذا الفهم بين الأوساط العلميّة وفي الرياضيات بالإضافة إلى بعض لغات البرمجة.(ملاحظة 1) يُمكن استخدم الرمز "log x" في بعض السياقات الأخرى للإشارة إلى اللوغاريتم ذو الأساس 10.
تاريخياً، أُدخلت الرموز "l." و "l" إلى الاستخدام منذ ثلاثينيات القرن الثامن عشر 1730s على الأقل،[2][3] وبقيت حتى أربعينيات القرن التاسع عشر 1840s على الأقل،[4] أما الرمز "log."[5] أو "log"،[6] فمنذ تسعينيات القرن الثامن عشر 1790s على الأقل. أخيراً، في القرن العشرين سُجِلَت الرموز "Log"[7] و "logh".[8]
أصل مصطلح اللوغاريتم الطبيعي
[عدل]
تنتج الدالة وذلك من أجل n ∈ ℤ تسلسل ثنائي لانهائيّ من النقاط يُمثّل قطعاً زائداً. عندما تُوصَل نقطتان متجاورتان إلى النقطة (0,0) بواسطة أشعة القطع الزائد، حينها يتشكَّل قطاع من هذا القطع الزائد، يكون لهذا القطاع منطقة وحدة "unit area". وبالتالي فإن المنطقة الكليّة الموجودة داخل القطع الزائد وخطوط مُقارباته منطقةٌ لانهائيّة، بما يتفق مع تباعد المتسلسلة المتناسقة. يتفق قياس المنطقة مع قياس القوس في كلا الدائرة والقطع الزائد الأيمن: ففي دائرة نصف قطرها √2 يكون لقوس القطاع الدائريّ زاوية تساوي منطقة القطاع. وبالمثل، تُقاس زاوية القطع الزائد للقوس القطع الزائديّ بالمنطقة الموافقة من قطاع القطع الزائد ذو المعادلة xy = 1.
يعود الفضل إلى ليونارد يولر الذي عرَّف بأهمية عدد يولر e=2.71828... كأساس للدالة الأسيّة واللوغاريتم الطبيعيّ. حيث أنه قدَّم لفكرة الدالة المتسامية لتصنيف الدوال المثلثيّة والأسيّة في كتاب مقدمة في تحليل اللانهاية (1748). يتطلَّب تقدير مساحة القطع الزائد اللوغاريتم الطبيعيّ، لذا كان يحول نقص التعبير عن تربيع القطع الزائد دون حساب التكامل، حتى وصفه جريجوري دي سانت-فينست (1647) بميزة لوغاريتميّة: إن توافق تسلسل حسابيّ من المناطق مع التسلسل الهندسيّ للمُقاربات. قادت توضيحات نيكولاس مركاتور وكريستيان هوغنس إلى مقدمة يولر التي فصَّلت الدوال الدائريّة من حيث السلسلة اللانهائيّة.
إن صلة الوصل بين المنطقة وأقواس الدائرة ودوال القطع الزائد تُظهر «طبيعيّة» اللوغاريتم.[9]
التعريفات
[عدل]
رسمياً، في حالة a يُمكن تعريف اللوغاريتم الطبيعيّ بأنه المنطقة تحت القطع الزائد 1/x. هذا هو التكامل
هذه الدالة لوغاريتم لأن توافق المبدأ الأساسيّ للوغاريتم:
يُمكن توضيح ذلك من خلال تقسيم التكامل الذي يُعرِّف ln(ab) إلى جزأين ومن ثُمّ المكاملة بالتعويض x = ta في الجزء الثاني، وفق الآتي:
في المصطلحات الأوليّة، هذا مجرد تحجيم بواسطة 1/a في الاتجاه الأفقيّ وبواسطة a في الاتجاه العموديّ. لا تتغير المنطقة تحت هذا التحوّل، ولكن يتم إعادة تشكيل المنطقة بين a و ab. لأن الدالة a/(ax) تُساوي الدالة 1/x، تكون المنطقة الناتجة بالضبط ln(b).
يُعرَّف العدد e بأنه عدد حقيقيّ فريد a حيث ln(a) = 1.
بدلاً من ذلك، إذا عُرِّفت الدالة الأسيّة أولاً، قل باستخدام سلسلة لانهائيّة، قد يُعرَّف اللوغاريتم الطبيعيّ بالدالة العكسيّة مثلاً ln هي كالدالة الآتية exp(ln(x)) = x. وبما أن مجال الدالة الأسيّة متزايد بحدّة، فإن ذلك مُحدَّد بشكل جيّد لجميع قيم x الإيجابيّة.
خاصيات
[عدل]اتصال ورتابة دالة اللوغاريتم الطبيعي
[عدل]نستنتج مما سبق ان الدالة ln معرفة على وقابلة للاشتقاق على هذا المجال و:
و منه الدالة ln متصلة على وبما ان مشتقتها موجبة قطعا فإنها تزايدية قطعا على
عمليات على دالة اللوغاريتم الطبيعي
[عدل]لتكن f دالة معرفة ب حيث a و x عددان موجبان قطعا. مشتقة هي نفس مشتقة دالة اللوغاريتم الطبيعي أي أن:
و بما ان: f(1) =k فان: ln(a)=k اذن وبصفة عامة:
من هذه الخاصية نستنتج الخاصيات التالية:
- (حالة خاصة)
حيث يشير الرمز إلى جداء.
الاشتقاق والمتسلسلات
[عدل]الإشتقاق
[عدل]يتم الحصول على مشتق اللوغاريتم الطبيعي كدالة ذات قيمة حقيقية على الأعداد الحقيقية الموجبة بواسطة:
إثبات
المتسلسلات
[عدل]إذا كان و ، فإن:[10]
هذه هي متسلسلة تايلور لـ ln x زائد 1. يؤدي تغيير المتغيرات إلى توليد متسلسلة ميركاتور:
صالحة من أجل |x| ≤ 1 و x ≠ −1.
دالة اللوغاريتم الطبيعي في التكامل
[عدل]بمكاملة دالة المقلوب، نتحصل على اللوغاريتم الطبيعي للقيمة المطلقة لـ x، بتعبير آخر:
و .
فيما يلي مثال في حالة g (x) = tan (x):
نعتبر f (x) = cos (x):
حيث sec (x) هي دالة القاطع.
حيث C هو ثابت التكامل. يمكننا مكاملة اللوغاريتم الطبيعي باستخدام التكامل بالتجزئة:
لتكن:
- إذن:
تكامل الدالة المركبة هو:
الكسور المستمرة
[عدل]في حين لا توجد كسور مستمرة بسيطة مُتاحة، فإن العديد من الكسور المستمرة المُعمَّمة هي، بما في ذلك:
- حيث تسمى المتسلسلة الأولى «متسلسلة مركاتور».
فهذه الكسور المستمرة، وبشكل محدد الأخير، هذه الكسور تتقارب للقيم القريبة من الواحد. على أي حال، يمكن حساب اللوغاريتمات الطبيعيّة لمعظم الأرقام الأكبر ببساطة عبر إضافة هذه الأرقام الأصغر بشكل متكرر، مع تقارب سريع مماثل. على سبيل المثال بما أن 2 = 1.253 × 1.024 يمكن حساب اللوغاريتم الطبيعيّ لِـ2 بالشكل الآتي:
علاوةً على ذلك، بما أن 10 = 1.2510 × 1.0243 فإن اللوغاريتم الطبيعيّ لِـ10 يمكن حسابه وبطريقة مُشابهة لما سبق، وفق الآتي:
اللوغاريتم العقدي
[عدل]يعرف كالآتي:
-
تمثيل z = abs(Im(ln(x + yi)))
-
تمثيل z = Re(ln(x + yi))
-
تمثيل z = abs(ln(x + yi))
-
تراكب الرسوم البيانية الثلاثة السابقة
انظر أيضًا
[عدل]هوامش
[عدل]ملاحظة 1: تتضمن هذه اللغات سي، وسي ++ و ساس [الإنجليزية] وماتلاب وماثماتيكا وفورتران وبايزيك.
مراجع
[عدل]- ^ O'Connor، J. J.؛ Robertson، E. F. (سبتمبر 2001). "The number e". The MacTutor History of Mathematics archive. مؤرشف من الأصل في 2019-08-14. اطلع عليه بتاريخ 2009-02-02.
- ^ Euler، Leonhard (1737). "Variae observationes circa series infinitas". Commentarii academiae scientiarum imperialis Petropolitanae (CASP) (نُشِر في 1744). ج. 9: 160–188. E72.
- ^ Euler، Leonhard (1925). Opera Omnia, Series Prima: Opera Mathematica. Teubner. ج. Quartum Decimum.
- ^ Cauchy، Augustin. Exercices d'analyse et de physique mathématique. ج. 3. ص. 380. مؤرشف من الأصل في 2015-09-05. اطلع عليه بتاريخ 2015-10-31.
- ^ Legendre، Adrien-Marie (1798). Essai sur la théorie des nombres. Paris, France: Duprat, libraire pour les mathématiques, quai des Augustins. ج. VI.
- ^ Landau، Edmund (1953) [1909]. Handbuch der Lehre von der Verteilung der Primzahlen (ط. 2). Berlin: Chelsea, New York.
- ^ Piskounov، Nikolaï [بالفرنسية] (1972). Calcul différentiel et intégral (ط. 5). Moskow: Editions Mir. ص. 91. مؤرشف من الأصل في 2015-11-17.
- ^ Jolley، L. B. W. (1961). Summation of Series (PDF) (ط. 2 (revised)). New York, USA: Dover Publications, Inc. LCCN:61-65274. مؤرشف من الأصل (PDF) في 2018-04-17. اطلع عليه بتاريخ 2015-10-31.
- ^ Ballew، Pat. "Math Words, and Some Other Words, of Interest". مؤرشف من الأصل في 2017-12-05. اطلع عليه بتاريخ 2018-01-18.
- ^ "Logarithmic Expansions" at Math2.org نسخة محفوظة 31 يوليو 2019 على موقع واي باك مشين.
| لوغاريتم طبيعي في المشاريع الشقيقة: | |
| |





![{\displaystyle ]0;+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a2b9afa8192cc3f8173fadddad0d1f5c499d881)

![{\displaystyle \mathbb {R} _{+}^{*}=]0;+\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/606c3de91fafde877b144126a329fc0b35534f03)








![{\displaystyle {\begin{aligned}\ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\,dx&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{a}^{ab}{\frac {1}{x}}\,dx\\[5pt]&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{1}^{b}{\frac {1}{at}}\,d(at)\\[5pt]&=\int _{1}^{a}{\frac {1}{x}}\,dx+\int _{1}^{b}{\frac {1}{t}}\,dt\\[5pt]&=\ln a+\ln b.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2b53dd1976a99950b5c8217d287c4af90d381d)



![{\displaystyle \forall (a;b)\in ]0:+\infty [^{2},\ \ln(ab)=\ln(a)+\ln(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b82a9f70dc4d37520a622aa11d284072b8940537)
![{\displaystyle \forall (a;b)\in ]0:+\infty [^{2},\ \ln \left({\frac {a}{b}}\right)=\ln(a)-\ln(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be7a5b58797e75ef324c761d5000fddeb7651f6e)
![{\displaystyle \forall a\in ]0;+\infty [,\ \forall n\in \mathbb {Z} ,\ \ln(a^{n})=n\ln(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b6f04d2e3f902b8050e7c7103f83607f21f2c1b)
![{\displaystyle \forall a\in ]0;+\infty [,\ \forall r\in \mathbb {Q} ,\ \ln(a^{r})=r\ln(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38cef3f3f5057e91f503c68cbb07f8afc8a63d8d)

![{\displaystyle \forall (a_{1},a_{2},....,a_{k})\in ]0:+\infty [^{k},\ \sum _{n=1}^{k}\ln(a_{n})=\ln(\prod _{n=1}^{k}a_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b986b1d2f8d3f8be67a75962fc87a625f45ce7ac)









![{\displaystyle {\begin{aligned}&\int \tan x\,dx=\int {\frac {\sin x}{\cos x}}\,dx\\[6pt]&\int \tan x\,dx=\int {\frac {-{\frac {d}{dx}}\cos x}{\cos x}}\,dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38c222fee8a371f1684e2d374d75332b7524269d)








![{\displaystyle {\begin{aligned}\ln(1+x)&={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots \\[5pt]&={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f9f9bda019d60b5ac5d5fd29ea2dd952c5b90a)
![{\displaystyle {\begin{aligned}\ln \left(1+{\frac {x}{y}}\right)&={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}\\[5pt]&={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90abfa2132828fc8eea5d3551dfa4df25dbdfa87)
![{\displaystyle {\begin{aligned}\ln 2&=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)\\[8pt]&={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc10de9595aca079ef56e7b76a2a23af56e453da)
![{\displaystyle {\begin{aligned}\ln 10&=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)\\[10pt]&={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/931b5e1a786450547bd77e466677d9a983974886)




