مماس

مماس

معلومات عامة

صنف فرعي من	خط مستقيم
جانب من جوانب	tangency (en)
تعريف الصيغة	$y=f(a)+f'(a)(x-a)$
ممثلة بـ	tangency (en)
لديه جزء أو أجزاء	point of tangency (en)

المستقيم الأحمر هو مماس المنحنى عند النقطة الحمراء

مستوى مماس لفلكة (أو كرة)

المماسُّ أو المستقيم الماسّ أو الخط المُماسّ هو خط يمر بنقطة وحيدة من دائرةٍ أو منحنى. المماس في حالة منحنى عام يُستخدم للتفاضل (Differential Calculus). مفهوم التماس هي واحد من أكثر المفاهيم الأساسية في الهندسة التفاضلية وجرى تعميمه على نطاق واسع، انظر فضاء مماس (Tangent space).

في الهندسة الوصفية

الفكرة البديهية لخط المماس للمنحنى هي فكرة الخط الذي "يلامس" المنحنى دون قطعه (تخيل المنحنى كما لو كان كيانا ماديًا لا يمكن اختراقه). الخط المستقيم الذي يقطع المنحنى يسمى قاطع.

علاوة على ذلك ، بالنظر إلى القاطع الذي يمر عبر نقطتين P و Q لمنحنى، يمكن اعتبار المماس عند P على أنه الخط المستقيم الذي يمر بالنقطة Q عندما تتطابق مع P.

هناك طريقة أخرى لرؤية مفهوم التماس من خلال التفكير في أن المماس عند نقطة P من منحنى γ هو الخط المستقيم الذي يشابه γ بالقرب من P.

حتى من هذه التعريفات غير الرسمية ، ندرك أنه قد تكون هناك حالات لا يتم فيها تعريف الخط المماس. على سبيل المثال ، إذا كان المنحنى ثلاثي وكان P رأسًا ، فلا يتوافق أي من التعريفين السابقين بشكل دقيق مع خط المماس المار بالنقطة P.

في الهندسة التركيبية، يمكن إعطاء تعريفات بديلة صارمة لخطوط مماس لمنحنيات محددة. على سبيل المثال ، يمكن تعريف الخط المتماس لدائرة دلتا مركزها O ونصف قطرها r عند نقطة P (تنتمي لمحيط دلتا) على أنه الخط الذي يمر عبر P على مسافة r من O، أو على أنه الخط الوحيد بالمستوى الذي يتشارك مع الدائرة النقطة P.

معلوم قطع مكافئ دلتا ونقطة P تنتمي إليه. مطلوب تحديد الخط p المتماس لدلتا في النقطة P. وبعبارة أخرى ، مطلوب تحديد الخط القطبي p لـلنقطة القطبية P بالنسبة لدلتا

في الهندسة متعددة الأبعاد ، يمكن تحديد المستوى المتماس لسطح بطريقة مماثلة (فضاء مماس).

لتحديد التماس في حالة المنحنى العام، يتم استخدام أدوات حساب التفاضل والتكامل متناهية الصغر بشكل عام.

معرض

• 
  وصلات مماسية بين دويريات مستوية
• 
  تحديد أحد المخروطيتين (باللون الأصفر) التي يشاركها ثلاث دويريات عامة. الدورية العامة هي التي تحيط مخروطيات غير متشابهة فيما بينها.
• 
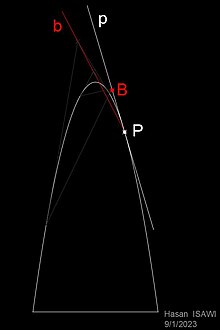
  تماس بين قطع مكافئ وقطع زائد
• 
  سلسلة من المخروطيات التي تشترك بثلاث نقاط وخط مماس

انظر أيضًا

• طريقة نيوتن
• ناظم السطح
• دائرة التقبيل
• مسألة أبولونيوس
• تعامد
• قاطع (منحنى).